MOEA/D: Multi-Objective Evolutionary Algorithm Based on Decomposition
CVPR Tutorial
Qingfu Zhang
June 19, 2023
MOEA/D=Decomposition + Collaboration
- Decomposition (from traditional opt)
- Decompose the task of approximating the PF into $N$ subproblems. Each subproblem can be single-objective or multiobjective.
- Collaboration (from swarm Intelligence and evolutionary computation)
- $N$ agents (procedures) are used. Each agent is for a different subproblem.
- These $N$ subproblems are related to one another. $N$ agents can solve these subproblems in a collaborative manner.
Major Issues

- Problem decomposition and neighborhood structure.
- Search method used by each agent: memory and reproduction operators.
- Collaboration: mating selection and replacement.
Basic MOEA/D
Problem Decomposition

- $\min g^{ws}(x|\lambda) = \lambda_1f_1(x) + \lambda_2f_2(x)$ where $\lambda_1 + \lambda_2 = 1$ and $\lambda_1, \lambda_2 \geq 0$.

Tchebycheff Approach
Optimization Problem
$$
\begin{aligned}
\min \text{ } &g^T(\mathbf{x} | \lambda, \mathbf{z}^{*}) \\
g^T(\mathbf{x} | \lambda, \mathbf{z}^{*}) &= \max\{ \lambda_1 |f_1(\mathbf{x}) - z_1^{*}|, \lambda_2| f_2(\mathbf{x}) - z_2^{*}|\} \\
\mathbf{z}^{*} &= (z_1^*, z_2^*) \text{ is a Utopian point. } \\
& z_1^{*} < \min f_1 \text{ and } z_2^{*} < \min f_2
\end{aligned}
$$

- For any Pareto optimal solution $\mathbf{x}^{*}$, there is a $\lambda$ such that $\mathbf{x}^{*}$ is optimal to the above problem.
- $g^T(\mathbf{x},\lambda)$ is not smooth w.r.t. $\mathbf{x}$,$\lambda$.
Weighted $L_p$ Approach
Optimization Problem
$$\begin{equation}
\begin{aligned}
\min \text{ } &g^T(\mathbf{x} | \lambda, \mathbf{z}^{*}) \\
\text{ where } & g^T(\mathbf{x} | \lambda, \mathbf{z}^{*}) = \left(\lambda_1| f_1(\mathbf{x}) - z_1^{*}|^p + \lambda_2| f_2(\mathbf{x}) - z_2^{*}|^p\right)^{\frac{1}{p}} \\
\mathbf{z}^{*} &= (z_1^*, z_2^*) \text{ is a Utopian point.} \nonumber
\end{aligned}
\end{equation}$$
- $p=1:$ weighted sum
- $p=\infty:$ Tchebycheff

Neighboring Subproblems
- Neighborhood: measure the relationship among the subtasks
- Two subproblems are neighbors if their weight vectors are close.
- Neighbouring subproblems should have similar objective functions and thus similar optimal solutions with high probability.
- Many different ways for defining neighborhood structure.
Decomposition, Neighborhood and Memory
- At each generation, each agent does the following:
- Mating selection: obtain the current solutions of some neighbours (collaboration).
- Reproduction: generate a new solution by applying reproduction operators on its own solution and borrowed solutions.
- Replacement:
- Replace its old solution by the new one if the new one is better than old one for its objective.
- Pass the new solution on to some of its neighbours, each of them replaces its old solution by this new one if it is better for its objective (collaboration, neighbourhood).
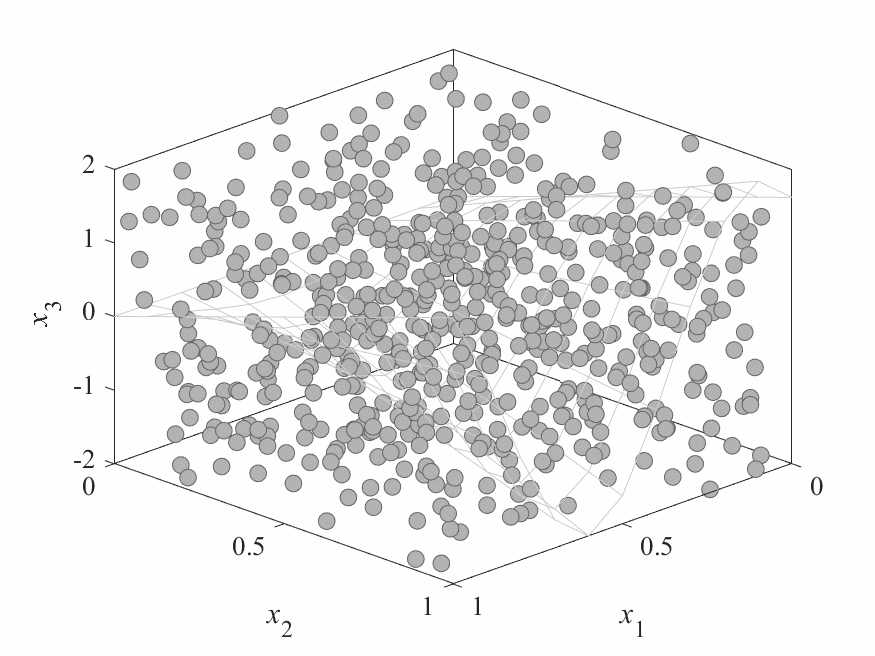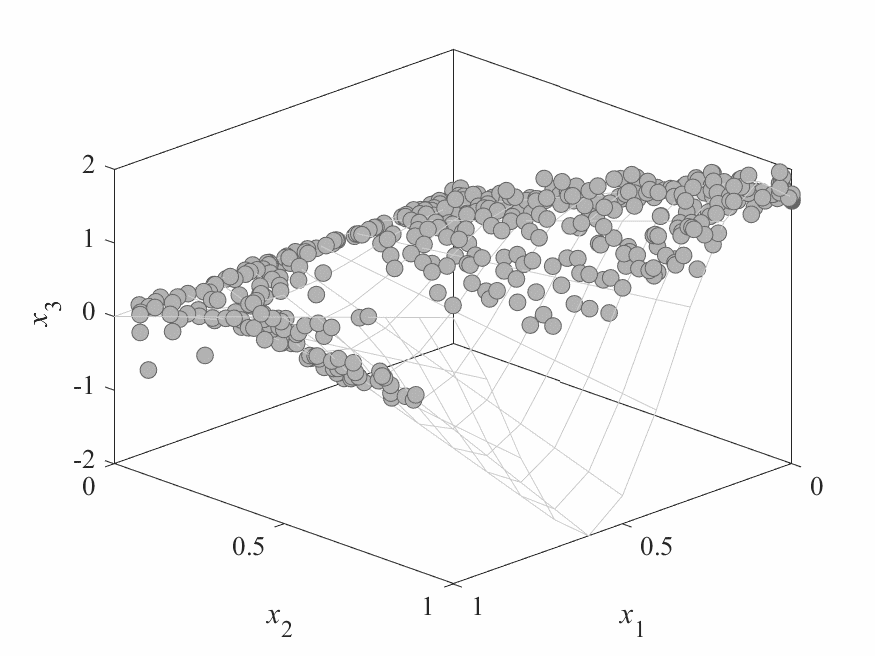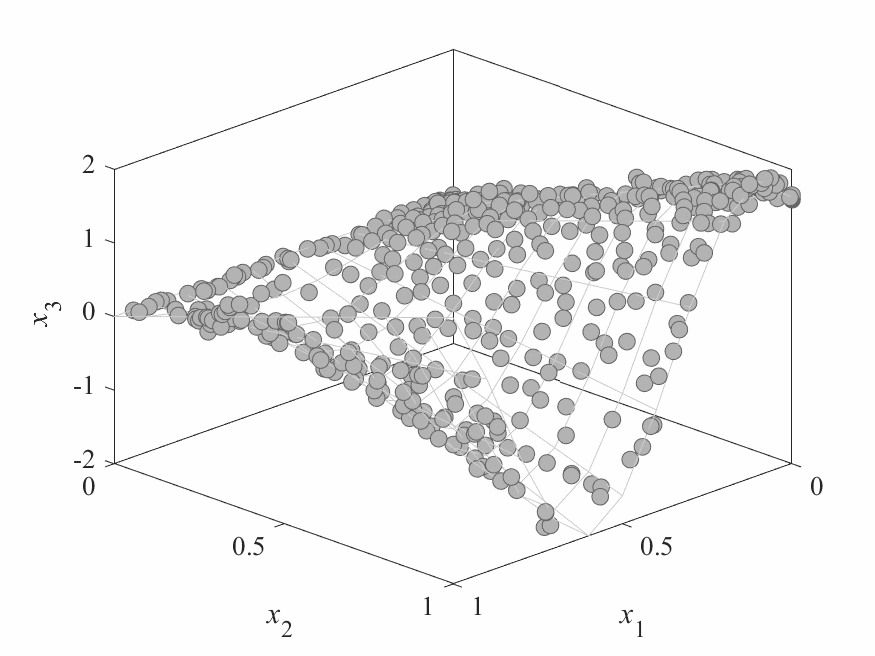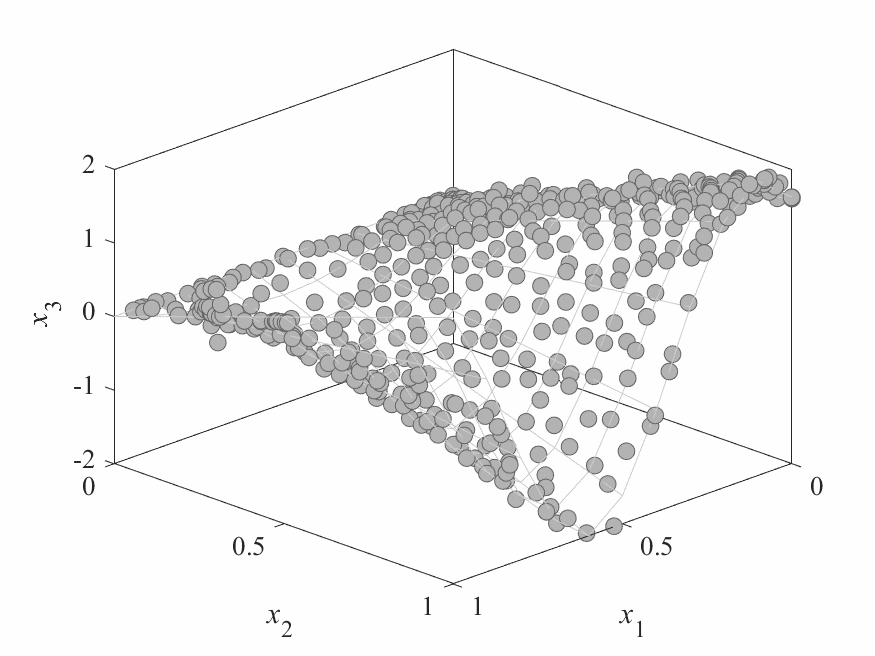
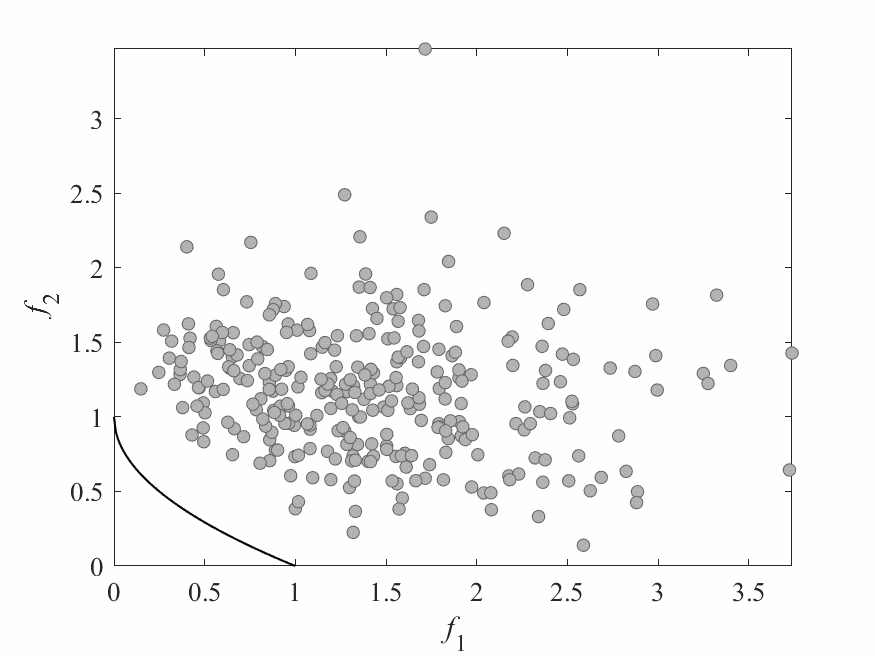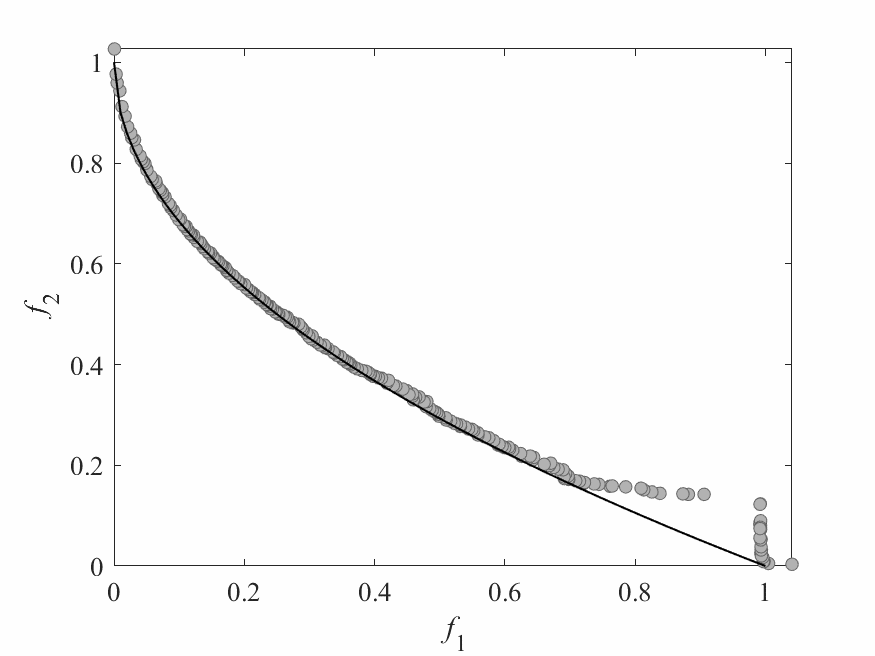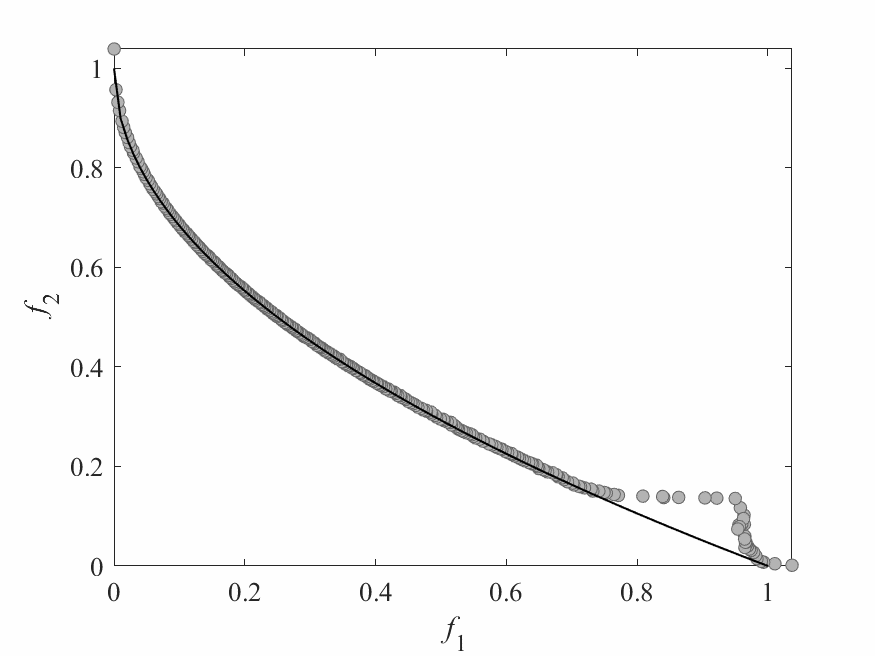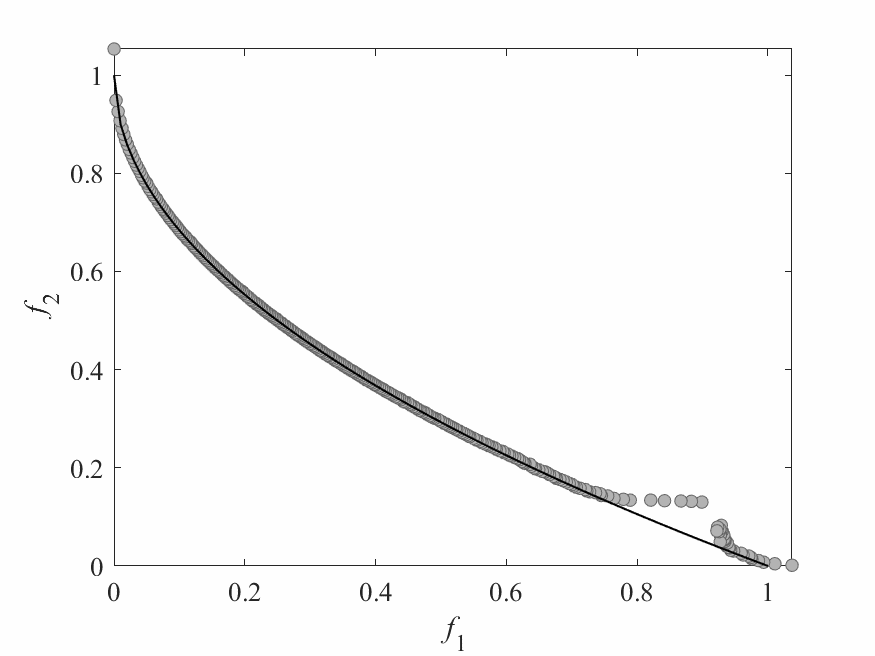
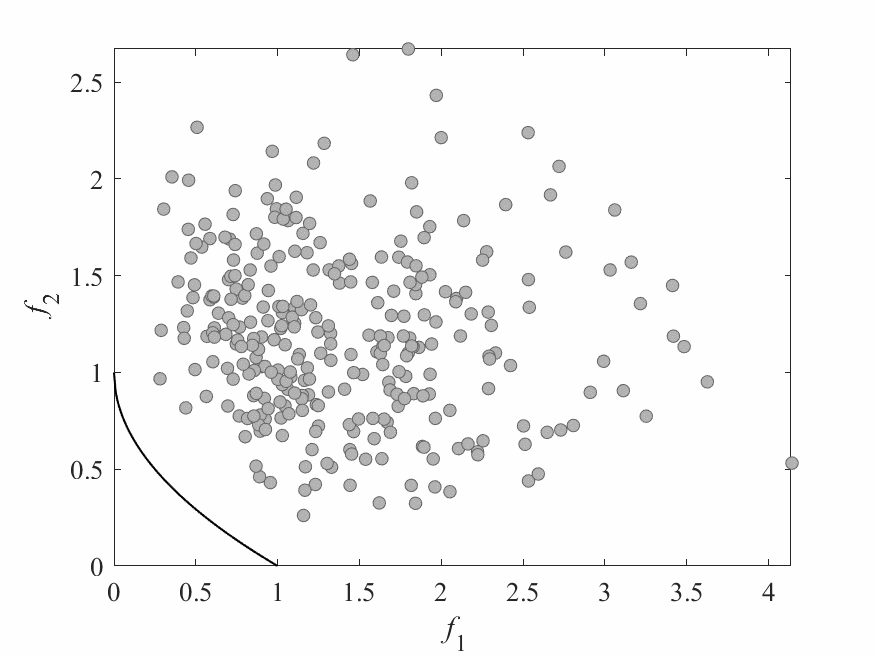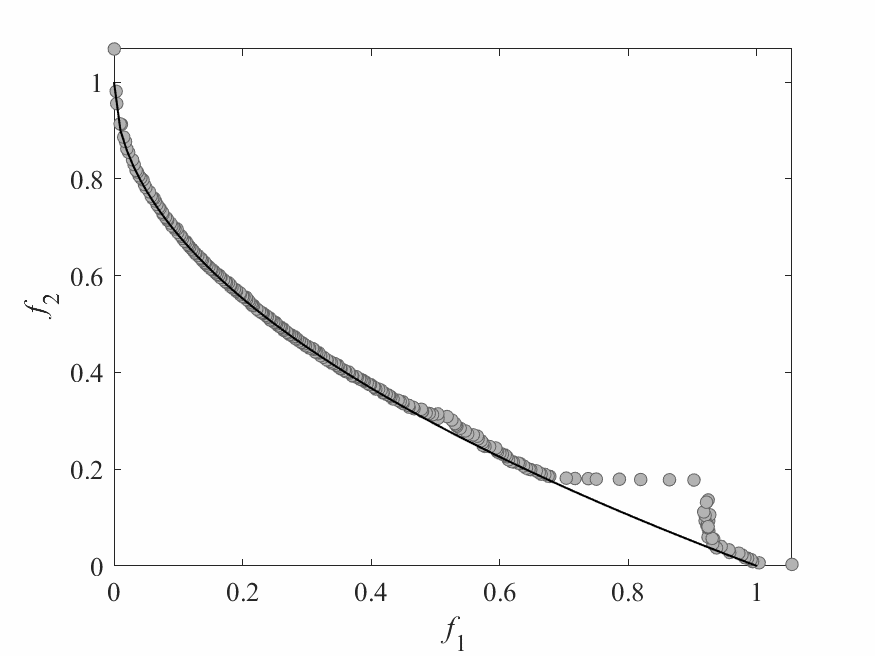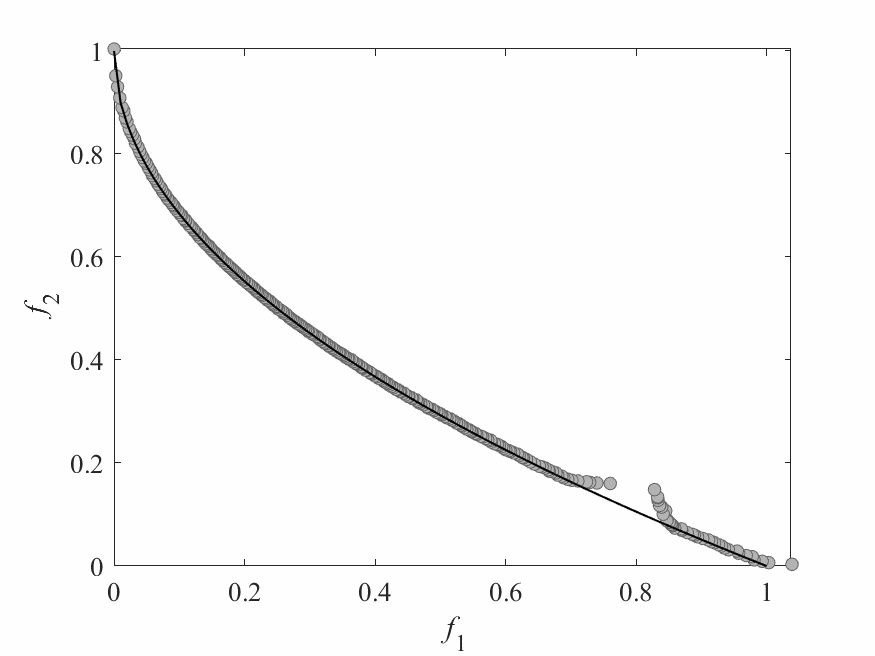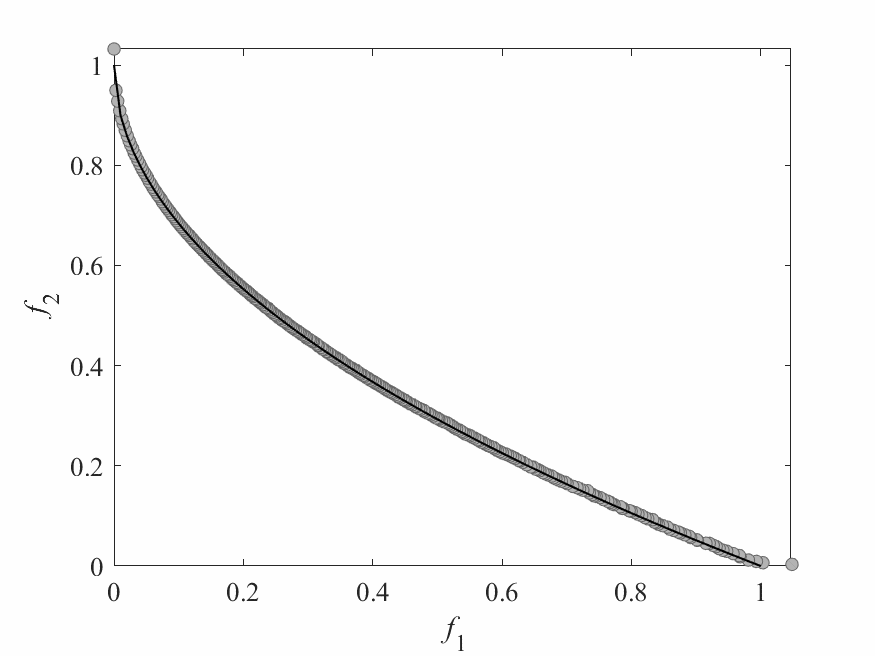
Simulation Results
- No of subproblems: 595, Reproduction operators: DE+Mutation
- No of generation: 500
- Test instance: $$ \begin{aligned} f_1 &= cos(0.5x_1\pi)cos(0.5x_x\pi) + \frac{2}{|J_1|}\sum_{j\in J_1}(x_j - 2x_2sin(2\pi x_1 + \frac{j\pi}{n}))^2 \\ f_2 &= cos(0.5x_1\pi)sin(0.5x_x\pi) + \frac{2}{|J_2|}\sum_{j\in J_1}(x_j - 2x_2sin(2\pi x_1 + \frac{j\pi}{n}))^2 \\ f_3 &= sin(0.5x_1\pi) + \frac{2}{|J_3|}\sum_{j\in J_3}(x_j - 2x_2sin(2\pi x_1 + \frac{j\pi}{n}))^2 \\ \end{aligned} $$
- $J_1 = {j|3\leq j \leq n, \text{ and } j-1 \text{ is a multiplication of 3}}$,
- $J_2 = {j|3\leq j \leq n, \text{ and } j-2 \text{ is a multiplication of 3}}$,
- $J_3 = {j|3\leq j \leq n, \text{ and } j \text{ is a multiplication of 3}}$
- Pareto Surface: $x_j = 2x_2\sin(2\pi x_1 + \frac{j\pi}{n}), j=3,\dots,n$
Dynamic Resource Allocation
- Different subproblems (agents) require different amounts of computational resources.
- Each subproblem (agent) has a utility value, which measures the likelihood of further improvement: \[ Utility = \frac{\text{The amount of improvement obtained}}{\text{The amount of computational resources used}} \]
- At each generation, a small number of agents are selected based on utility values and receive computational resources.
Simulation Results
- Test instance: $$ \begin{aligned} f_1 &= x_1 + \frac{2}{|J_1|}\sum_{j \in J_1}\left(x_j - 0.8x_1\cos\left(6\pi x_1 + \frac{j\pi}{n}\right)\right)^2 \\ f_2 &= 1 - \sqrt{x}_1 + \frac{2}{|J_2|}\sum_{j\in J_2}\left(x_j - 0.8x_1\sin\left(6\pi x_1 + \frac{j\pi}{n}\right)\right)^2\\ \end{aligned} $$ Pareto Surface: $x_j = \begin{cases} 0.8x_1\cos\left(6\pi x_1 + \frac{j\pi}{n}\right) & j \in J_1 \\ 0.8x_1\sin\left(6\pi x_1 + \frac{j\pi}{n}\right) & j \in J_2 \end{cases}$
- No of subproblems: 300
- Reproduction operators: DE+Mutation
- No of generation: 100
Additional Remarks
- Diversity among subproblems leads to diversity among $\{\mathbf{x}^1, \mathbf{x}^2,\dots,\mathbf{x}^N\}$
- MOEA/D has a well-organized memory.
- Each agent can adopt other search methods such as heuristics (e.g., EDA, ACO and tabu search) or gradient based search.
- Agents can be divided into several groups. Each group share some common info such as probability models.
More on Decomposition Methods
Penalty based boundary interaction (PBI) (Zhang & Li 2007)
Optimization Problem
$$
\begin{aligned}
\min \text{ } &g^T(\mathbf{x} | \lambda, \mathbf{z}^{*}) = d_1 + \theta d_2 \\
s.t. & x \in \Omega
\end{aligned}
$$
- $\mathbf{z}^*,\lambda$ define a line direction.
- $\theta > 0$ is the penalty parameter

- $\theta \rightarrow \infty \Rightarrow \text{PBI} \rightarrow$ NBI (Normal boundary Interaction) (Das, 1998).
- Different Pareto optimal solutions can be obtained by using different direction lines.
Penalty based boundary interaction (PBI) (Zhang & Li 2007)
- Diversity and Convergence:
Optimization Problem
$$
\begin{aligned}
\min \text{ } &g^T(\mathbf{x} | \lambda, \mathbf{z}^{*}) = d_1 + \theta d_2 \\
s.t. \text{ } & x \in \Omega
\end{aligned}
$$
- $d_1$: convergence
- $d_2$: diversity

- It has been used in EMO algorithm design such as in:
- I-DBEA (2015)
- MOEA/D-DU (2016)
- $\theta$-DEA (2016)
Penalty based boundary interaction (PBI) (Zhang & Li 2007)
- Other Variants:
Optimization Problem
$$
\begin{aligned}
\min \text{ } &g^T(\mathbf{x} | \lambda, \mathbf{z}^{*}) = d_1 + \theta d_2 \\
s.t. \text{ } & x \in \Omega
\end{aligned}
$$

- $d_2$ can be replace by $\alpha$ (Chen et al, 2016)
- $g$ can be replaced by other functions (Ishibuchi et al, 2016, Chen et al 2016)
- NSGA-III = Pareto dominance (for convergence) + decomposition ($d_2$ for diversity) (Deb et al, 2013).
Inverted PBI (IPBI, Sato 2014)
Optimization Problem
\[
\max g^{IPBI}(x|\lambda, z^*) = d_1 - \theta d_2
\]
- $z^+$ should be above the PF (nadir point)
- Difference between PBI and IPBI:
- When PF=ABC, some different subproblems in IPBI have the same optimal solutions.
- When PF=DEF, some different subproblems in PBI have the same optimal solutions.


Constrained Decomposition

- Single objective decomposition (Wang et al, 2015)
Optimization Problem
$$
\begin{aligned}
\min g(x) &= aggregation(f_1, f_2) \\
s.t. \text{ } & F(x) \in \Omega_i
\end{aligned}
$$
- Good for diversity
- Multiple-objective to multiple-objective (M2M) (Liu et al, 2014)
Optimization Problem
$$
\begin{aligned}
& \min(f_1, f_2) \\
& s.t. \text{ } F(x) \in \Omega_i
\end{aligned}
$$
- MOEA/D-M2M: Each agent can uses an EMO algorithm.
Other Variants
MOEA/D for Expensive Multiobjective Optimization
- Expensive opt: function evaluation = expensive computer/physical experiments.
- The computational budget could be very limited, say, 200 function evaluations.
- Efficient Global Optimization (Bayesian Optimization) for single optimization problem do the following iteration:
- Using the evaluated solutions, build a probabilistic model $p(f│x)$ for objective $f(x)$.
- Use $p(f|x)$ to define acquisition function $\phi(x)$ (which measures the merits of figure of evaluation of objective $f$ at $x$.
- Maximize $\phi(x)$ to obtain $\bar{x}$, evaluate it.
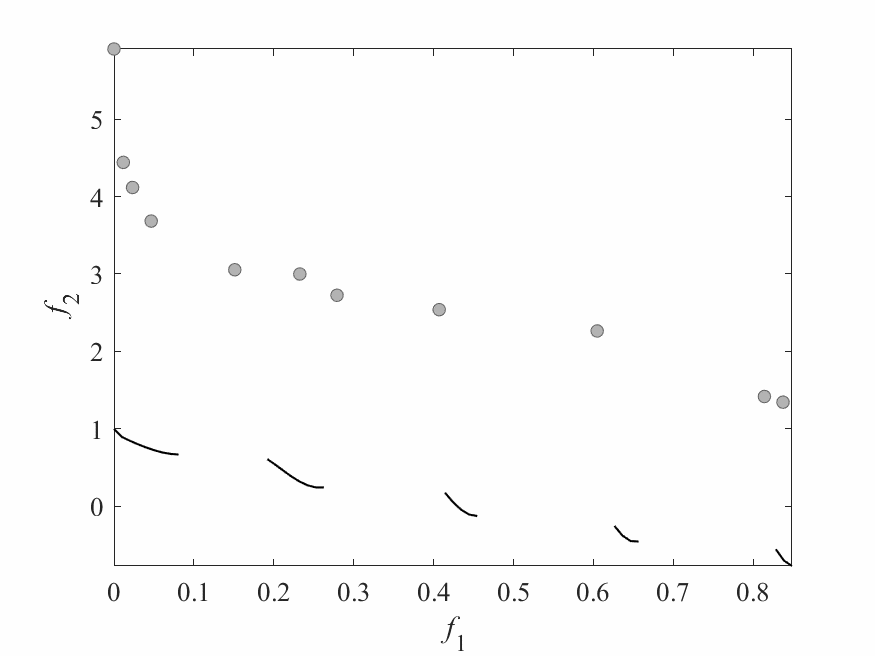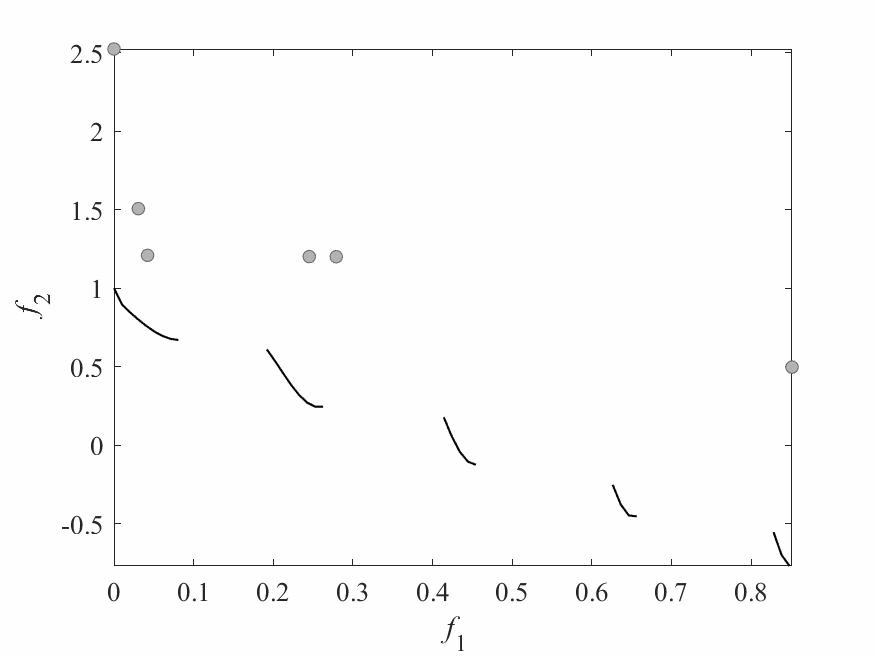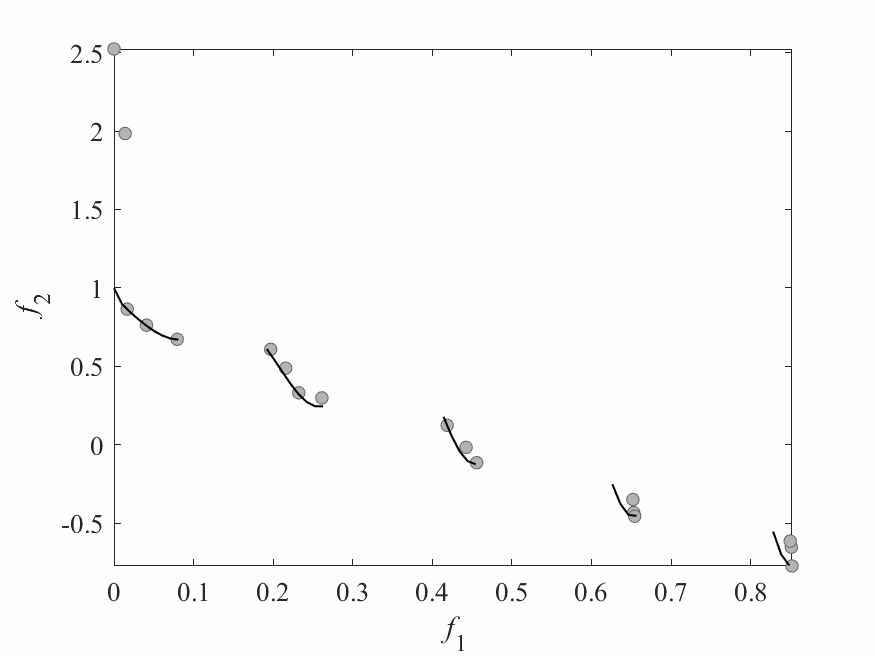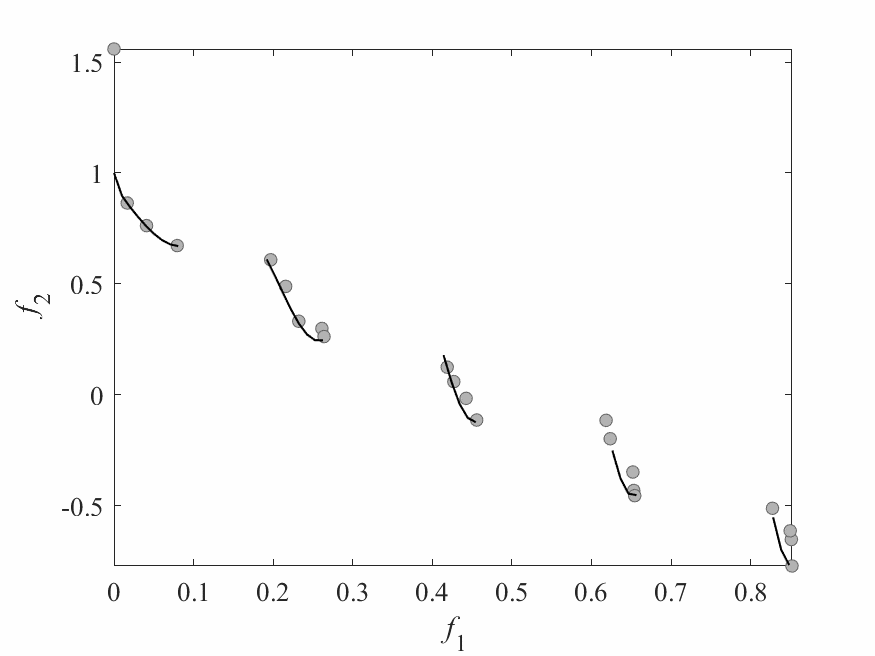
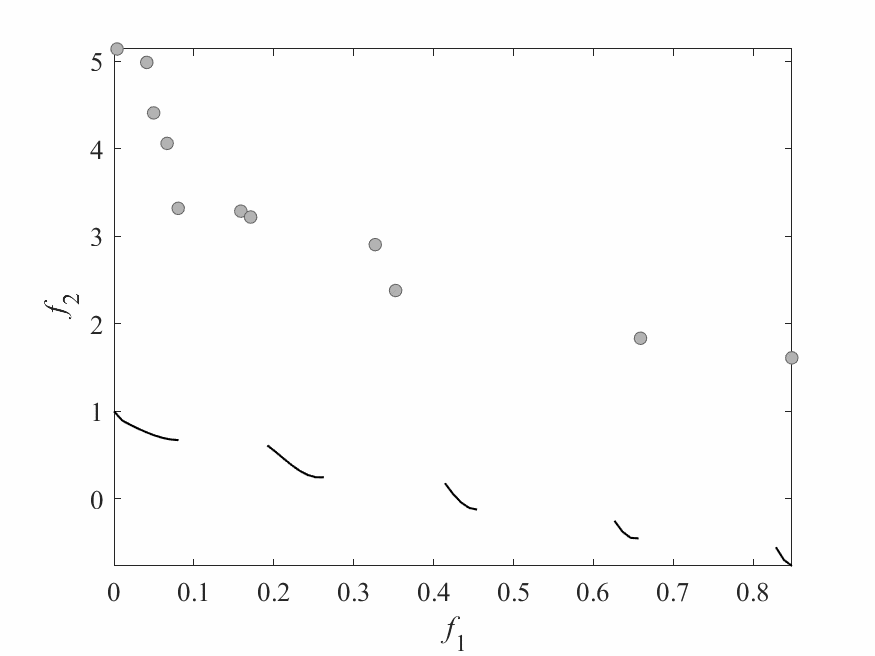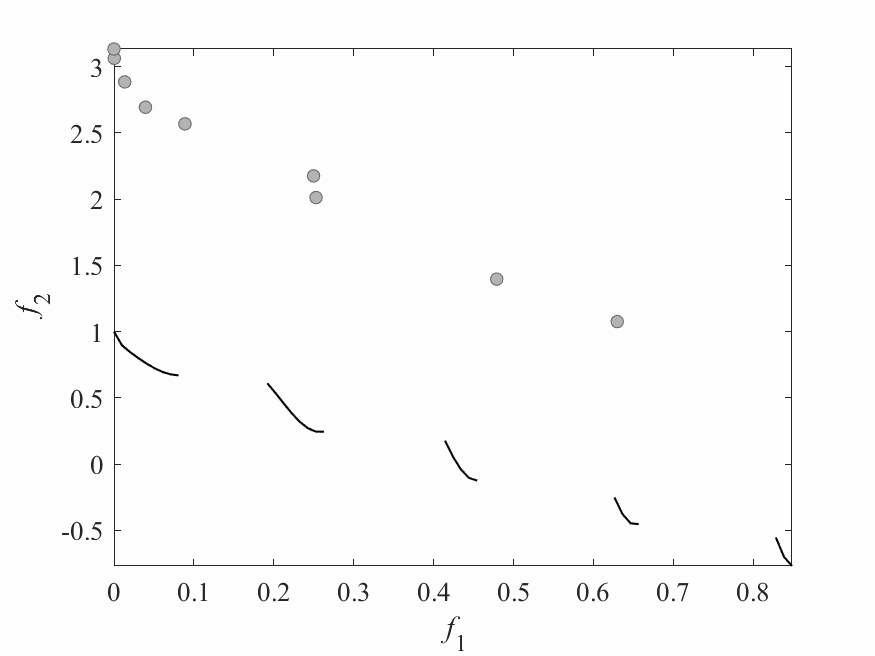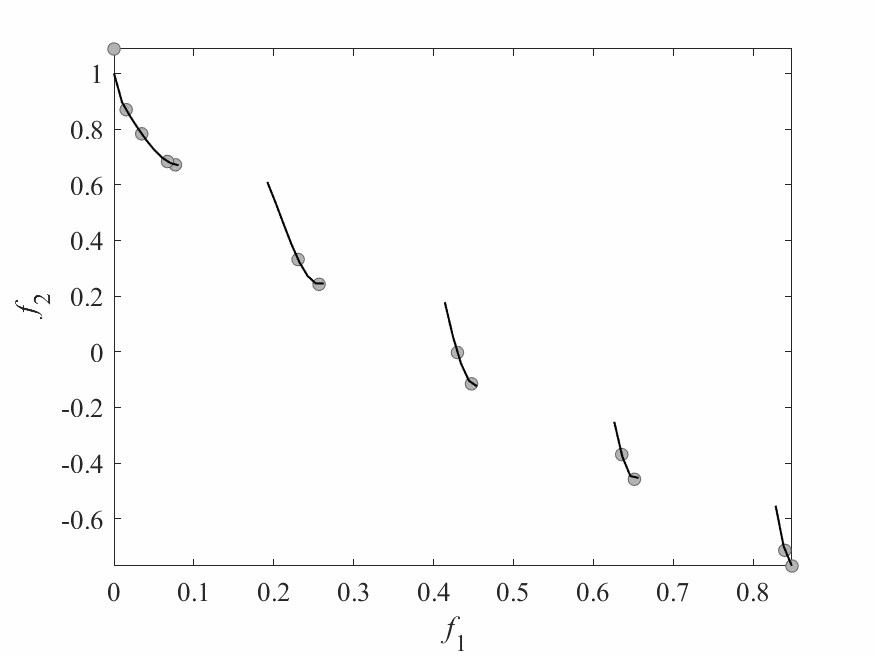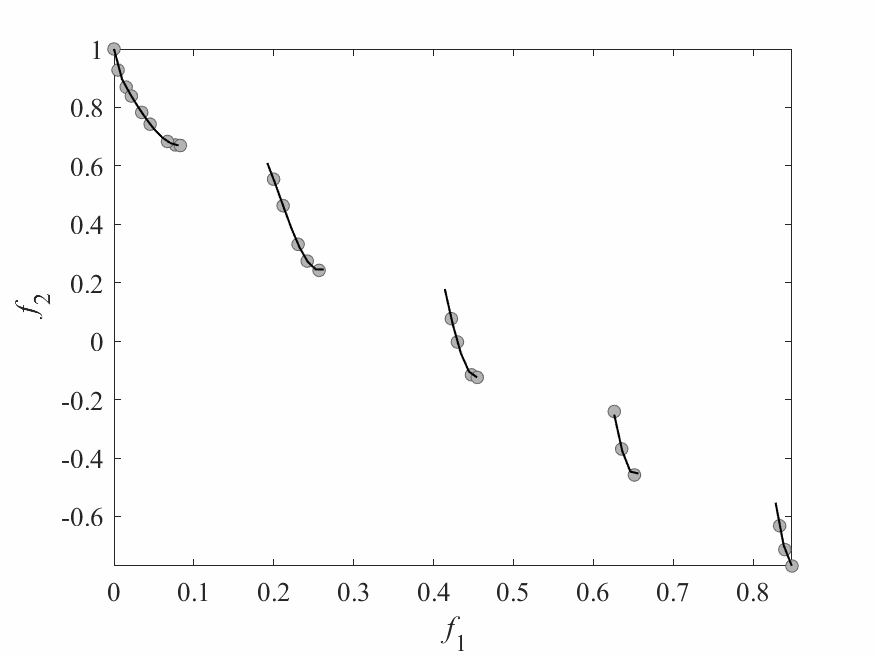
Experimental Results
- Experiments:
- ZDT3: 2 objectives and 6 decision variables.
- Computational budget: 150 function evaluations
PLS/D for Discrete Optimization
- Decompose the objective space into a number of sub-regions.
- Each subregion i is associated with an aggregated objective function: \[ \text{e.g., } g_{ws}(x, w_i) = 0.4f_1(x) + 0.6f_2(x) \]
- Agent i searches Subregion i by using a PLS guided by $g_{ws}(x, w_i)$.
- J. Shi, Q. Zhang, J Sun, PLS/D, IEEE Trans on Cybernetics, 2019
Experimental Results
- Test problem: multiobjective Unconstraint Binary Quadratic Programming
- Reproduction operators: Pareto local search (PLS)
- No of variables = 200. No. of objectives: 2 and 3
- No. of regions = 11 (for 2-obj) and 66 (for 3-obj)
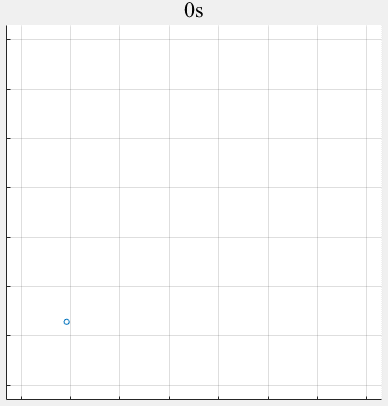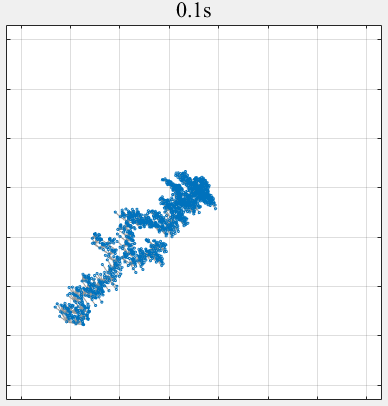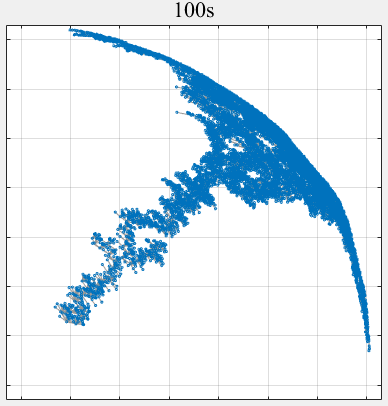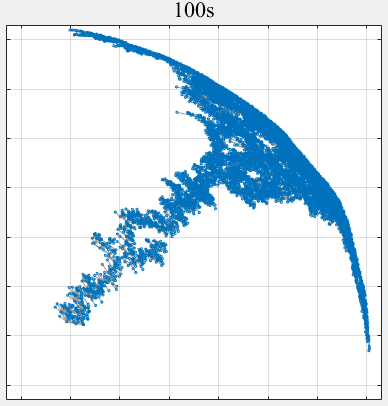
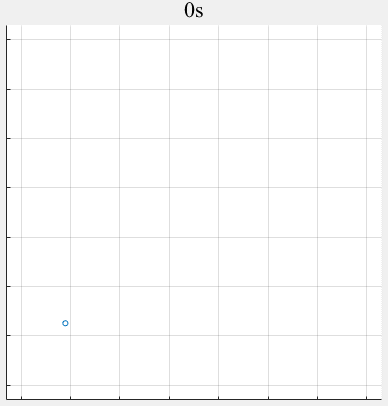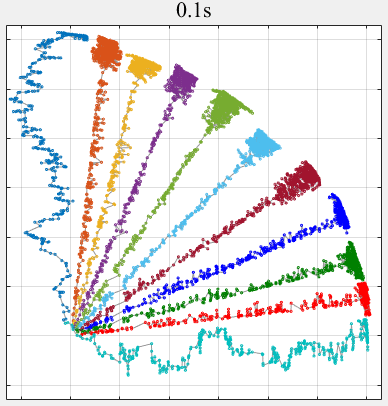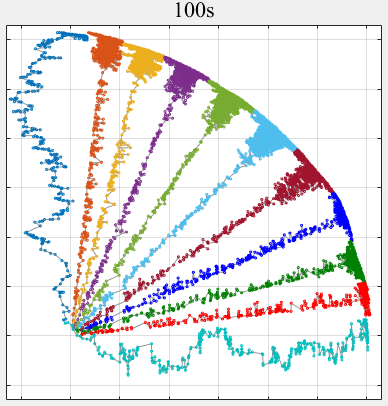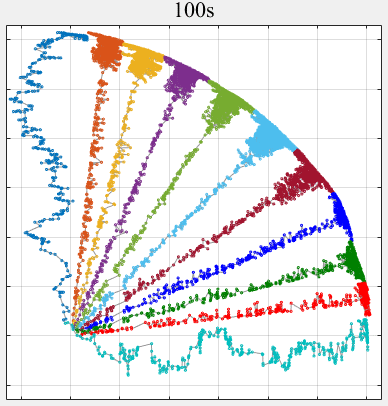


- PPLS/D: Parallel Pareto Local Search Based on Decomposition, IEEE Transactions on Cybernetics, 2020
Resources
Survey Papers on MOEA/D


Survey Papers on MOEA/D


Conclusions
- MOEA/D= Decomposition + Collaboration, a methodology for multiobjective optimization.
- Key design issues: decomposition, search method for each agent, collaboration.
- Different single optimization methods can be readily used in MOEA/D framework.
- Multiobjective optimization methods can also be integrated in MOEA/D framework.
