Multi-Objective Optimization for Deep Learning
CVPR Tutorial
June 19, 2023
Standard Optimization in Deep Learning
- Empirical Risk Minimization $$\underset{\theta}{\operatorname{arg min}} \frac{1}{T} \sum_t l\left(f(\mathbf{x}^t;\mathbf{\theta}),\mathbf{y}^t\right) + \lambda\Omega(\mathbf{\theta})$$
- Goal: find a single optimal solution
- Differentiable loss functions and regularizer.
- cross-entropy, hinge loss, MSE, $l_2$, $l_1$, etc.

Emerging Class of Optimization Problems
- Multi-Objective Optimization $$ \underset{\theta}{\operatorname{arg min}} (f_1(\mathbf{X};\theta), f_2(\mathbf{X};\theta), \ldots, f_k(\mathbf{X};\theta))$$
- Feature: objectives may be in conflict with each other
- Goal: find a multiple pareto-optimal solutions
- Loss functions: may or may not be differentiable
- Optimization variables: continuous, discrete, mixed interger, etc.
Where do multiple objectives arise in machine learning?
Application (1): Fairness: Utility-Fairness Trade-Off

- Objectives:
- accuracy
- demographic parity violation
- On Characterizing the Trade-off in Invariant Representation Learning, TMLR 2022
Application (2): Explainability: Accuracy-Explainability Trade-Off

- It's Just Not That Simple: An Empirical Study of the Accuracy-Explainability Trade-off in Machine Learning for Public Policy, FAccT 2022
Application (3): Neural Architecture Search

- Lu et. al. Neural Architecture Transfer, TPAMI 2021
Application (4): Multi-Task Learning

- Sener and Koltun, Multi-Task Learning as Multi-Objective Optimization, NeurIPS 2018.
Application (5): Neural Networks over Encrypted Data

- Wei and Boddeti, AutoFHE: Automated Adaption of CNNs for Efficient Evaluation over FHE, Cryptology ePrint Archive 2023
Application (6): Discovering Learning Algorithms from Scratch


- Guha et. al. MOAZ: A Multi-Objective AutoML-Zero Framework, GECCO 2023
Application (7): Learning Robotic Adaptation Policies from Scratch

- Kelly et. al. Discovering Adaptable Symbolic Algorithms from Scratch, IROS 2023
Most Common Solution Multi Objective Optimization
Weighted Sum Scalarization
$$ \begin{aligned} \min & \text{ } g^{ws}(x|\lambda) = \lambda_1f_1(x) + \lambda_2f_2(x) \\ s.t. & \text{ } \lambda_1 + \lambda_2 = 1 \\ & \text{ } \lambda_1, \lambda_2 \geq 0 \end{aligned} $$
- Solve optimization problem separately for each choice of $\lambda$.
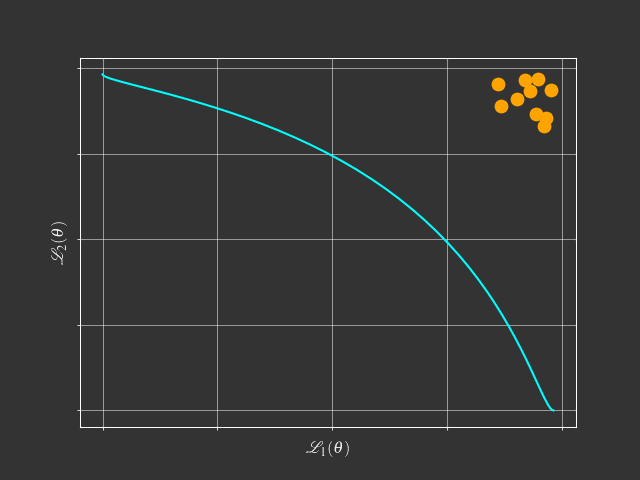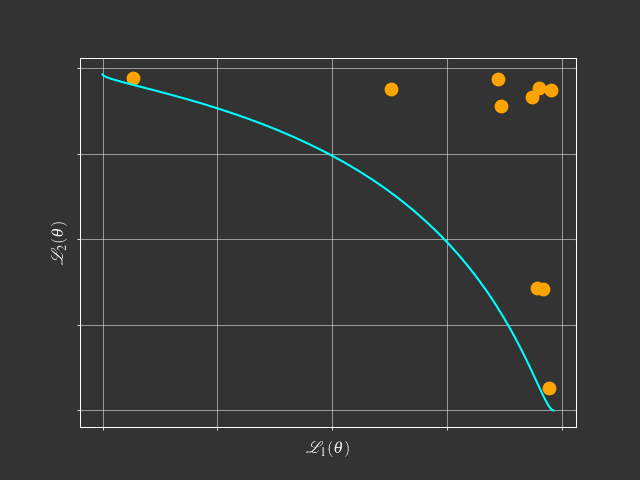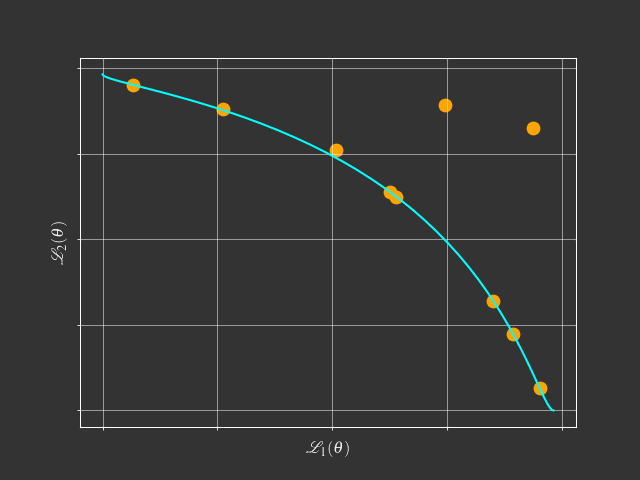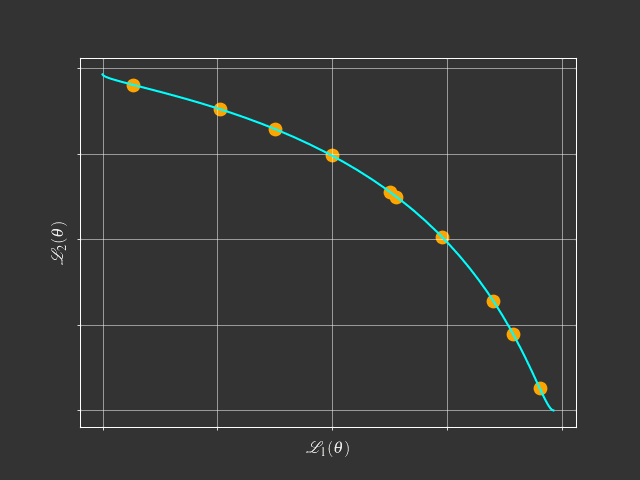
The problem with scalarization
$$ \begin{aligned} \min & \text{ } g^{ws}(x|\lambda) = \lambda_1f_1(x) + \lambda_2f_2(x) \\ s.t. & \text{ } \lambda_1 + \lambda_2 = 1 \\ & \text{ } \lambda_1, \lambda_2 \geq 0 \end{aligned} $$What is this tutorial about?
Going beyond scalarization


Foundational Concepts


A Few Applications



Hands-On Demo






