Multi-Objective Optimization for Multi-Task Learning


CVPR Tutorial

Xi Lin

June 19, 2023

Outline


  • Finding a Single Pareto Solution

  • Finding a Set of Pareto Solutions

  • Building a Model for the Whole Pareto Set

  • Rethinking MOO for MTL and Future Directions

Finding a Single Pareto Solution

Multi-Task Learning (MTL)

    • MTL: Solve multiple related tasks at the same time
      • MTL Loss
      \[\min_{\theta} \mathcal{L}(\theta) = \sum_{i} w_i\mathcal{L}_i(\theta)\]

Drawbacks of MTL Loss

MTL Loss
\[\min_{\theta} \mathcal{L}(\theta) = \sum w_i\mathcal{L}_i(\theta)\] \[\min_{\theta} \mathcal{L}(\theta) = \sum {\color{yellow}{w_i}}\mathcal{L}_i(\theta)\] \[\min_{\theta} \mathcal{L}(\theta) = \sum w_i\color{cyan}{\mathcal{L}_i(\theta)}\] \[\min_{\theta} \mathcal{L}(\theta) = \color{orange}{\sum} w_i\mathcal{L}_i(\theta)\]
  • Weights:
    • Manually chosen by practitioners
    • Exhaustive search might be needed
  • Tasks:
    • Might be conflicted with each other
    • No single best solution
  • Simple Weighted-Sum:
    • Can't find any solution on concave Pareto front

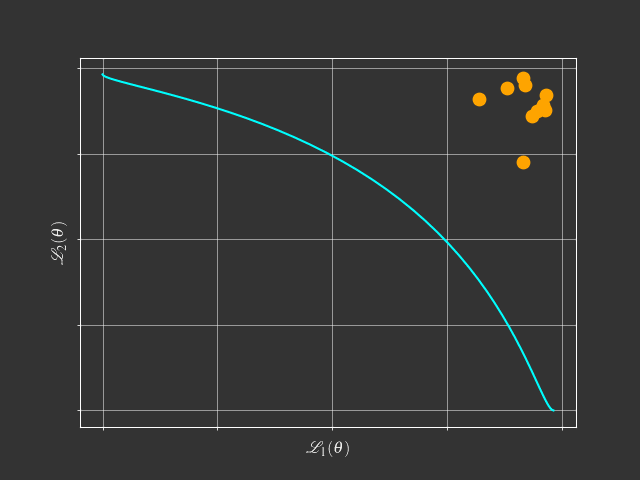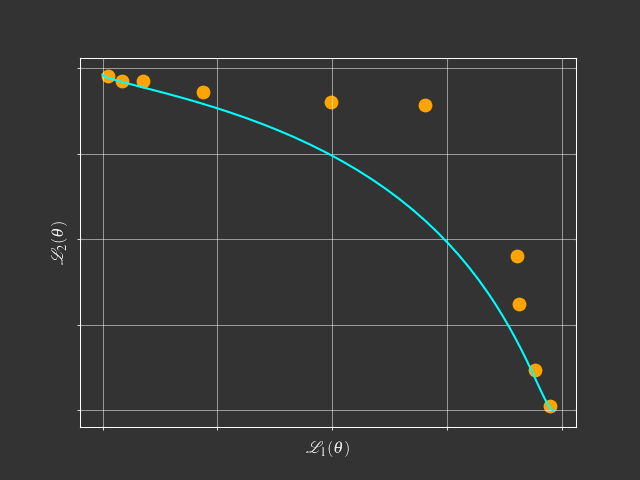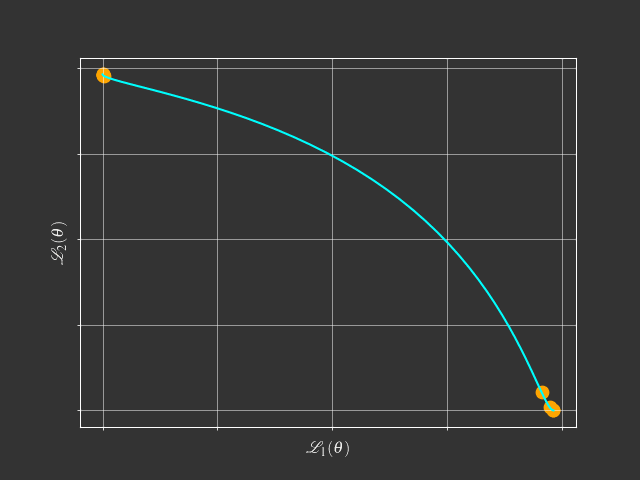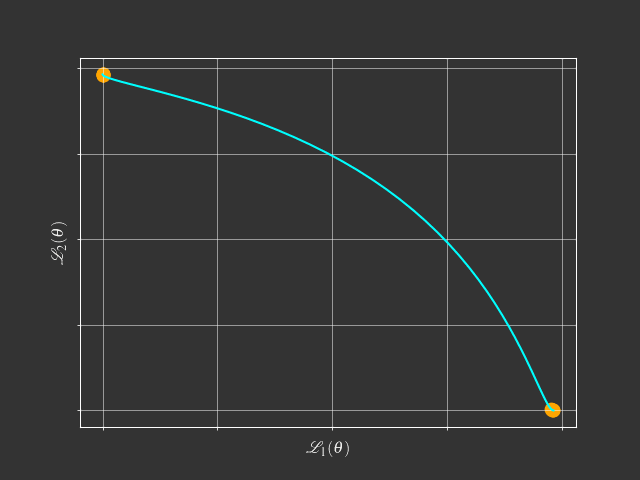
View Point of Multi-Objective Optimization

$$\min_{\theta} \mathcal{L}(\theta) = (\mathcal{L}_1(\theta),\mathcal{L}_2(\theta),\dots,\mathcal{L}_m(\theta))$$
    • Goal: Find a Pareto optimal solution for MTL with gradient-based method
    • Motivation: Karush-Kuhn-Tucker (KKT)Condition$^{[1,2]}$
There exist $\alpha_1, \dots, \alpha_m \geq 0$ such that $\sum_{i=1}^m \alpha_i = 1$ and $\sum_{i=1}^m \alpha_i \nabla \mathcal{L}_i(\theta) = 0$

    • Any $\theta$ that satisfies this condition is called a Pareto stationary solution.

  • Sener and Koltun, Multi-Task Learning as Multi-Objective Optimization, NeurIPS 2018.
  • $^1$Fliege and Svaiter, Steepest descent methods for multicriteria optimization, Mathematical Methods of Operations Research 2000.
  • $^2$Schäffler et. al., Stochastic method for the solution of unconstrained vector optimization problems. Journal of Optimization Theory and Applications 2002.

Multi-Gradient Descent Algorithm (MGDA)

$$\min_{\theta} \mathcal{L}(\theta) = (\mathcal{L}_1(\theta),\mathcal{L}_2(\theta),\dots,\mathcal{L}_m(\theta))$$
    • Goal: Find a Pareto optimal solution for MTL with gradient-based method
    • Method: Multi-Gradient Descent Algorithm (MGDA)$^{1}$
$$ \begin{equation} \min_{\alpha_1,\dots,\alpha_m} \left\{\left\|\sum_{i=1}^m \alpha_i\nabla_{\theta}\mathcal{L}_i(\theta)\right\|_2^2 \Bigg\rvert \sum_{i=1}^m \alpha_i=1, \alpha_i\geq 0 \text{ } \forall i\right\} \nonumber \end{equation} $$

  • A: $\underbrace{\left\|\sum_{i=1}^m \alpha_i\nabla_{\theta}\mathcal{L}_i(\theta)\right\|_2^2}_{\text{Pareto Stationary Solution}} = 0$
  • Optimization: Frank-Wolfe algorithm$^2$ to obtain $d=\sum_{i=1}^m\alpha_i\nabla_{\theta}\mathcal{L}_i(\theta)$
  • Sener and Koltun, Multi-Task Learning as Multi-Objective Optimization, NeurIPS 2018.
  • $^1$Jean-Antoine Désidéri, Multiple-gradient descent algorithm (MGDA) for multiobjective optimization, Comptes Rendus Mathematique 2012.
  • $^2$Martin Jaggi, Revisiting Frank-Wolfe: Projection-Free Sparse Convex Optimization, ICML 2013.

Linear Scalarization vs MGDA

Linear Scalarization

  • Sener and Koltun, Multi-Task Learning as Multi-Objective Optimization, NeurIPS 2018.
  • Jean-Antoine Désidéri, Multiple-gradient descent algorithm (MGDA) for multiobjective optimization, Comptes Rendus Mathematique 2012.
  • Martin Jaggi, Revisiting Frank-Wolfe: Projection-Free Sparse Convex Optimization, ICML 2013.

Promising Performance of Pareto Solution for MTL


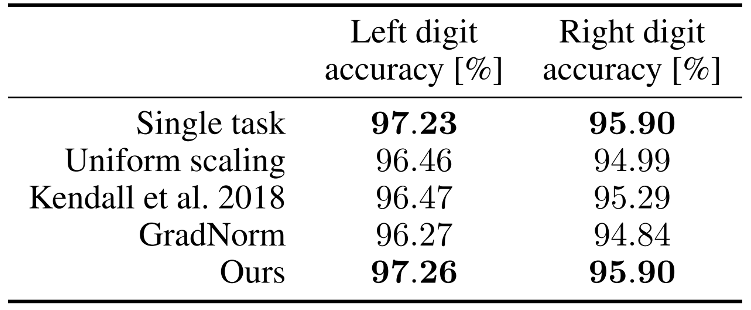
  • MultiMNIST: MTL version of MNIST Classification
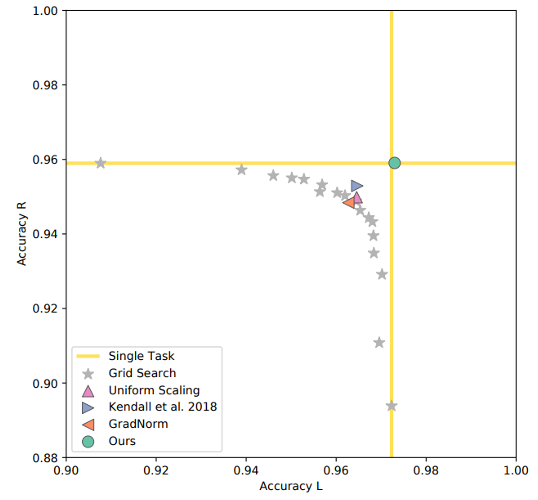
  • Sener and Koltun, Multi-Task Learning as Multi-Objective Optimization, NeurIPS 2018.
  • Sabour, Frosst, and Hinton, Dynamic Routing Between Capsules, NeurIPS 2017.

Promising Performance of Pareto Solution for MTL

  • Cityscapes Scene Understanding:
    • Semantic Segmentation
    • Instance Segmentation
    • Depth Estimation
  • Sener and Koltun, Multi-Task Learning as Multi-Objective Optimization, NeurIPS 2018.
  • Cordts et. al., The Cityscapes Dataset for Semantic Urban Scene Understanding, CVPR 2016.

Different Ways to Find the Gradient

    • PCGrad: Gradient Surgery for Multi-Task Learning, NeurIPS 2020.
    • CAGrad: Conflict-Averse Gradient Descent for Multi-task Learning, NeurIPS 2021.
    • I-MTL: Towards Impartial Multi-Task Learning, ICLR 2020.
    • RotoGrad: Gradient Homogenization in Multitask Learning, ICLR 2022.
    • Nash-MTL: Multi-Task Learning as a Bargaining Game, ICML 2022.
    • MoCo: Mitigating Gradient Bias in Multi-Objective Learning, ICLR 2023.
  • Related Work on Weight Adjustment:
    • Uncertainty: MTL Using Uncertainty to Weigh Losses for Scene Geometry and Semantics, CVPR 2018.
    • GradNorm: Gradient Normalization for Adaptive Loss Balancing, ICML 2018.
    • DWA: End-to-End Multi-Task Learning with Attention, CVPR 2019.
    • Just Pick a Sign: Optimizing Deep Multitask Models with Gradient Sign Dropout, NeurIPS 2020.

Finding a Set of Pareto Solutions

There are Many Pareto Solutions

Linear Scalarization
Adaptive Methods
Pareto MTL
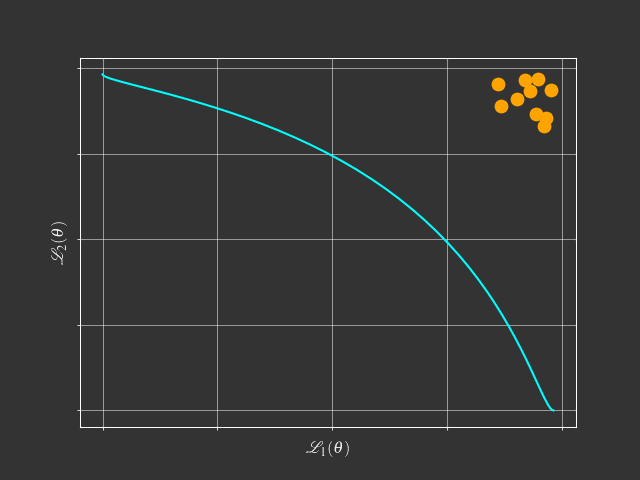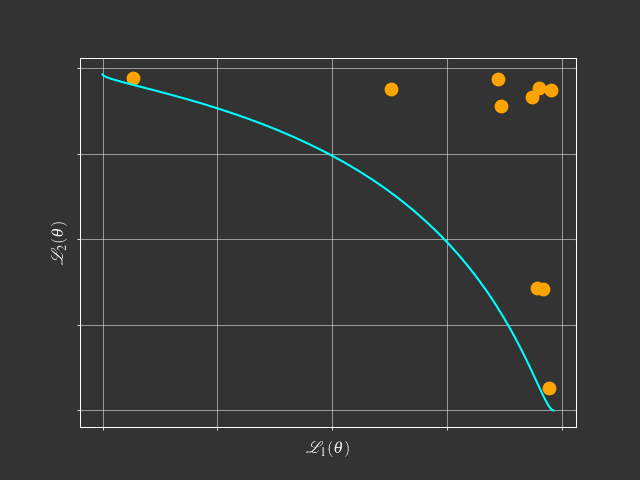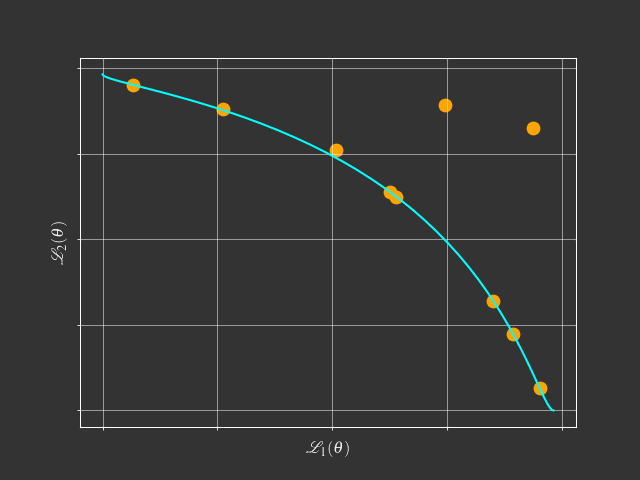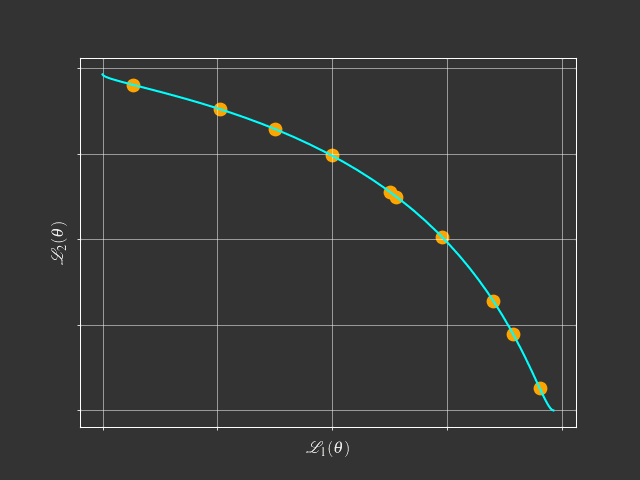
    • Pareto Solutions represent different trade-offs among tasks
    • Fixed Linear Scalarization can't find the concave Pareto front.
    • Adaptive Methods can find a single solution.
    • Pareto MTL can find a set of diverse Pareto solutions.
  • Lin et. al., Pareto Multi-Task Learning, NeurIPS 2019

Pareto Multi-Task Learning

  • Goal: Find:
    • a Pareto optimal solution
  • Method:
Decompose MTL into multiple subproblems
$$ \begin{equation} \begin{aligned} \min_{\theta} \quad & \left(\mathcal{L}_1(\theta),\mathcal{L}_2(\theta),\dots,\mathcal{L}_m(\theta)\right) \\ \text{s.t.} \quad & \mathbf{\mathcal{L}(\theta)} \in \Omega_k = \{\mathbf{v} \in \mathbb{R}^{m}_+ | \mathbf{u}^T_j\mathbf{v} \leq \mathbf{u}^T_k\mathbf{v}, \forall j \in \{1, \dots, K\}\} \nonumber \end{aligned} \end{equation} $$
Idea borrowed from MOEA/D and MOEA/D-M2M
Decompose MTL into multiple subproblems
$$ \begin{equation} \begin{aligned} \min_{\theta} \quad & \left(\mathcal{L}_1(\theta),\mathcal{L}_2(\theta),\dots,\mathcal{L}_m(\theta)\right) \\ \text{s.t.} \quad & \mathbf{\mathcal{L}(\theta)} \in \Omega_k = \{\mathbf{v} \in \mathbb{R}^{m}_+ | \mathbf{u}^T_j\mathbf{v} \leq \mathbf{u}^T_k\mathbf{v}, \forall j \in \{1, \dots, K\}\} \nonumber \end{aligned} \end{equation} $$
Rewrite constraint: $\mathbf{G}_j(\theta_t)=(\mathbf{u}_j-\mathbf{u}_k)^T\mathbf{\mathcal{L}(\theta_t)} \leq 0, \forall j \in \{1, \dots, K\}$

KKT Condition for Restricted Pareto Stationary Solution
There exist $\alpha_i \geq 0, \beta_i \geq 0 \text{ } \forall i,j$ such that $\sum_{i}\alpha_i + \sum_{j}\beta_j = 1$ and $\sum_i \alpha_i \nabla \mathcal{L}_i(\theta) + \sum_j \beta_j\mathbf{\mathcal{G}_j}(\theta) = 0$
Find a gradient direction for each subproblem
$$ \begin{equation} \min_{\alpha_i,\beta_j, \forall i,j} \left\{\left\|\sum_{i} \alpha_i\nabla_{\theta}\mathcal{L}_i(\theta)+\sum_{j} \beta_j\nabla_{\theta}\mathcal{G}_i(\theta)\right\|_2^2 \Bigg\rvert \sum_{i} \alpha_i + \sum_j \beta_j=1, \alpha_i\geq 0,\beta_j \geq 0 \text{ } \forall i,j\right\} \nonumber \end{equation} $$
  • Lin et. al., Pareto Multi-Task Learning, NeurIPS 2019.
  • Zhang and Li, MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition, TEVC 2007.
  • Liu et.al., Decomposition of a Multiobjective Optimization Problem Into a Number of Simple Multiobjective Subproblems, TEVC 2013.
  • Fliege and Svaiter, Steepest descent methods for multicriteria optimization, Mathematical Methods of Operations Research 2000.

Diverse Pareto Sets for MTL Problems

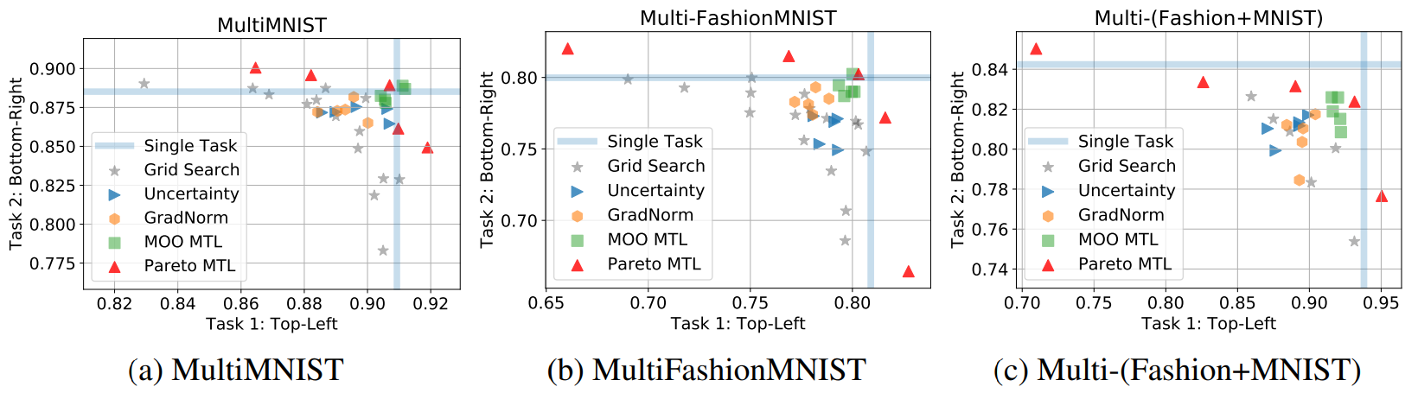
  • Sabour, Frosst, and Hinton, Dynamic Routing Between Capsules, NeurIPS 2017
  • Xiao et. al., Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning Algorithms, arXiv 2017

Other Methods to Find Diverse Pareto Solutions

    • Exact Pareto Optimal (EPO) Search, ICML 2020.
    • Weighted Chebyshev-MGDA (XWC-MGDA), NeurIPS 2021.
    • Hypervolume (HV) Maximization, EMO 2023.
    • Efficient Continuous Pareto Exploration, ICML 2020.
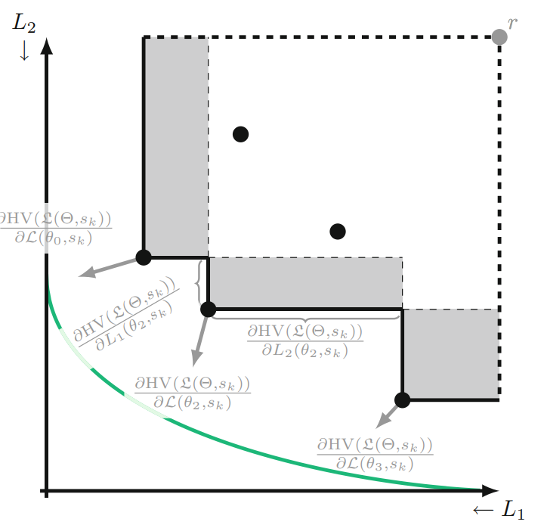
    • Tchebycheff Procedure for Multi-task Text Classification, ACL 2020.
    • Multi-Objective Stein Variational Gradient Descent (MO-SVGD), NeurIPS 2021.
    • The Stochastic Multi-Gradient Algorithm for MOO and its Application to Supervised Machine Learning, Annals of Operations Research 2021.
    • Pareto Navigation Gradient Descent: a First-Order Algorithm for Optimization in Pareto Set, UAI 2022.
    • Stochastic Multiple Target Sampling Gradient Descent, NeurIPS 2022.

Building a Model for the Whole Pareto Set

There could be Infinite Pareto Solutions

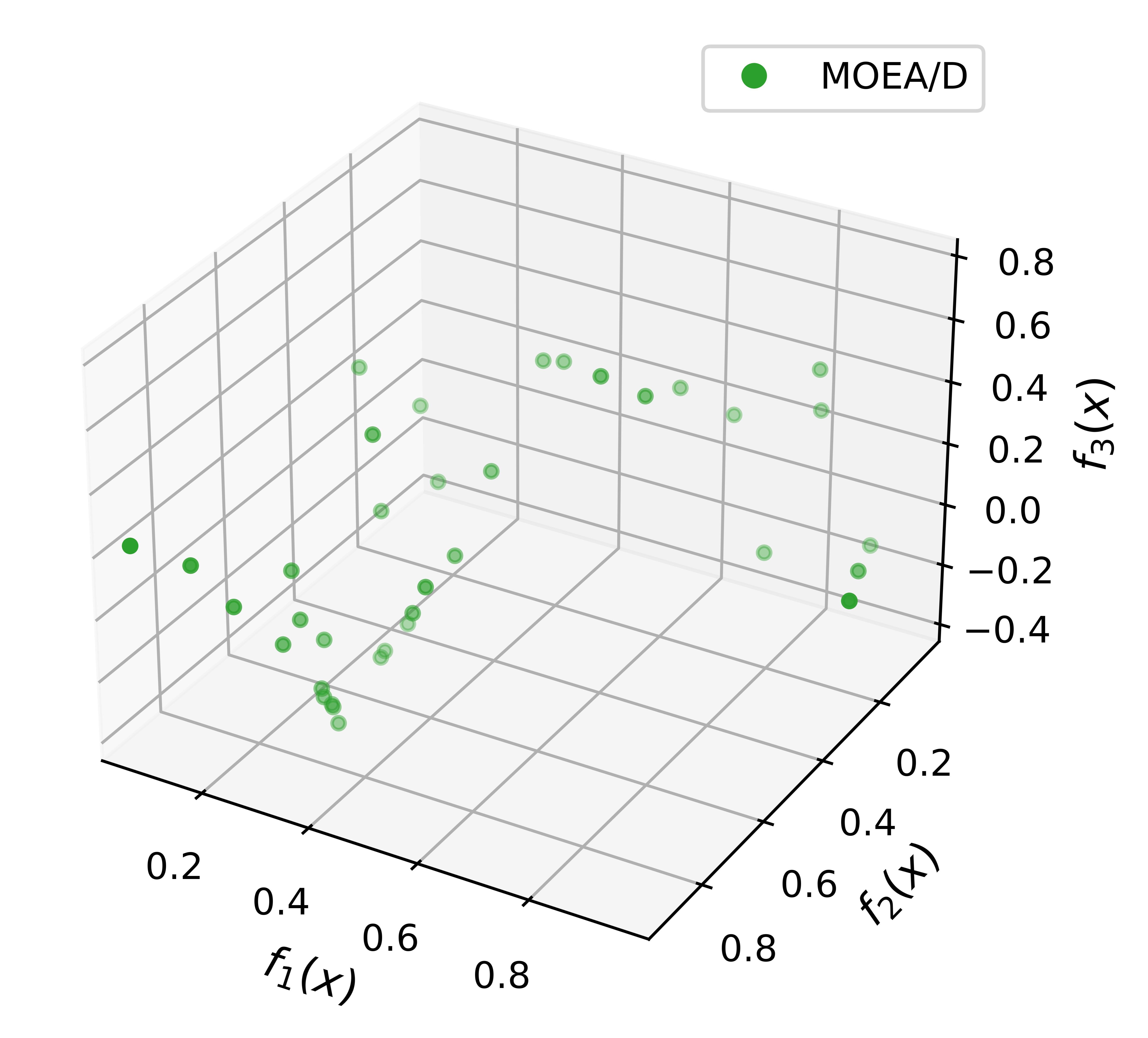
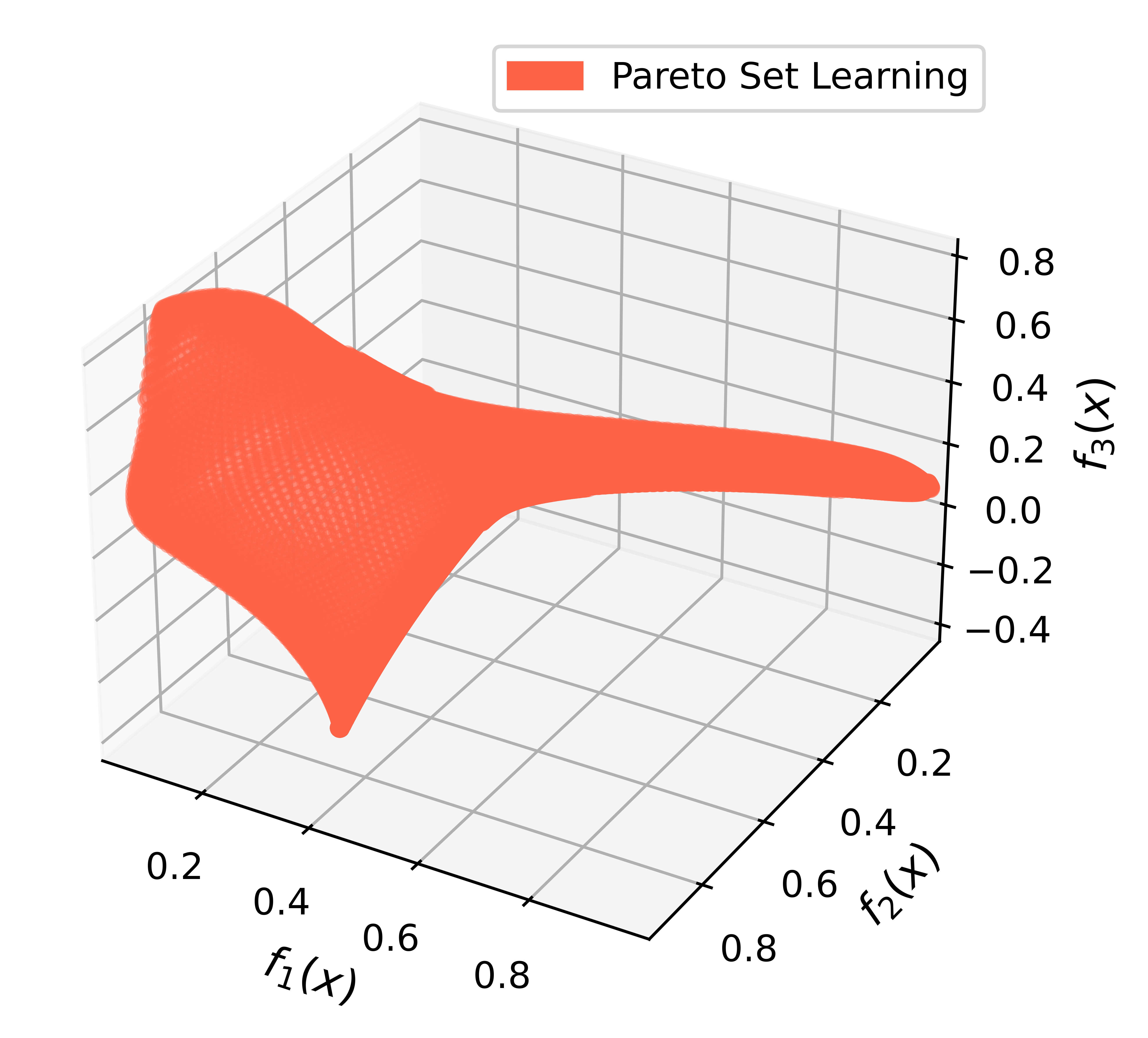
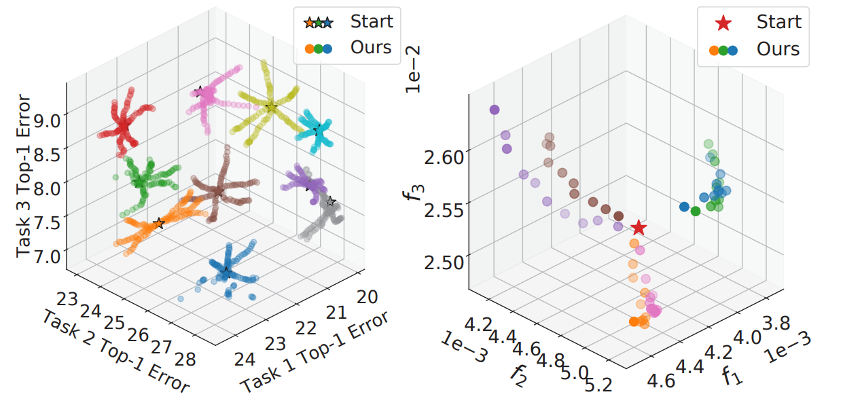
    • A few solutions cannot cover the whole Pareto front
    • Storing many solutions lead to high computational/memory cost
  • Ma and Du et.al., Efficient Continuous Pareto Exploration in Multi-Task Learning, ICML 2020.

Learning the Whole Pareto Set/Front

  • Goal: Find a,
    • Pareto optimal solution
    • set of diverse Pareto solutions
    • model to approximate the whole Pareto set
  • Navon and Shamsian et. al., Learning the Pareto Front with Hypernetwork, ICLR 2021.
  • Lin et. al., Controllable Pareto Multi-Task Learning, arXiv 2021.

Preference-Conditioned Pareto Set Model

  • Goal: Build a model to approximate the whole Pareto set
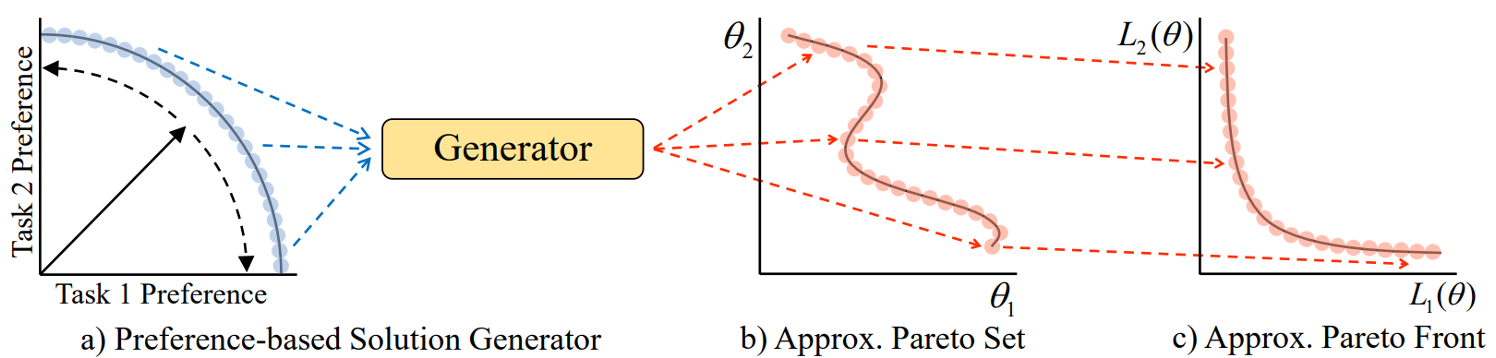
  • By adjusting the preferences, decision-makers can explore any trade-off Pareto solutions on the approximate Pareto set/front.
  • Navon and Shamsian et. al., Learning the Pareto Front with Hypernetwork, ICLR 2021.
  • Lin et. al., Controllable Pareto Multi-Task Learning, arXiv 2021.

HyperNetwork-based Pareto Set Model

  • Goal: Build a model to approximate the whole Pareto set
  • Method: Preference-conditioned Hypernetwork
Pareto HyperNetwork (PHN)$^1$
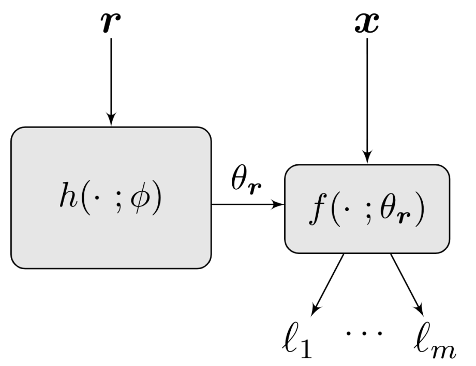
  • $^1$Navon and Shamsian et. al., Learning the Pareto Front with Hypernetwork, ICLR 2021.
  • $^2$Lin et. al., Controllable Pareto Multi-Task Learning, arXiv 2021.
  • Ha et. al., HyperNetworks, ICLR 2017.

Learning the Whole Pareto Set

Linear Scalarization
Adaptive Methods
Pareto MTL
Pareto Set Learning

Learned Pareto Sets for MTL Problems

  • Navon and Shamsian et. al., Learning the Pareto Front with Hypernetwork, ICLR 2021.

Other Methods for Learning the Pareto Front

    • COSMOS: Conditioned One-shot Multi-Objective Search, ICDM 2021.
    • Controllable Dynamic Multi-Task Architectures, CVPR 2022.
    • Learning a Neural Pareto Manifold Extractor with Constraints, UAI 2022.
    • Multi-Objective Deep Learning with Adaptive Reference Vectors, NeurIPS 2022.
    • Improving Pareto Front Learning via Multi-Sample Hypernetworks, AAAI 2023.

Rethinking MOO for MTL and Future Directions

Is Adaptive Weight Beneficial for Finding a Single Solution? Is MTL Truely Multi-Objective?

  • Simple linear scalarization can achieve state-of-the-art performance$^{123}$
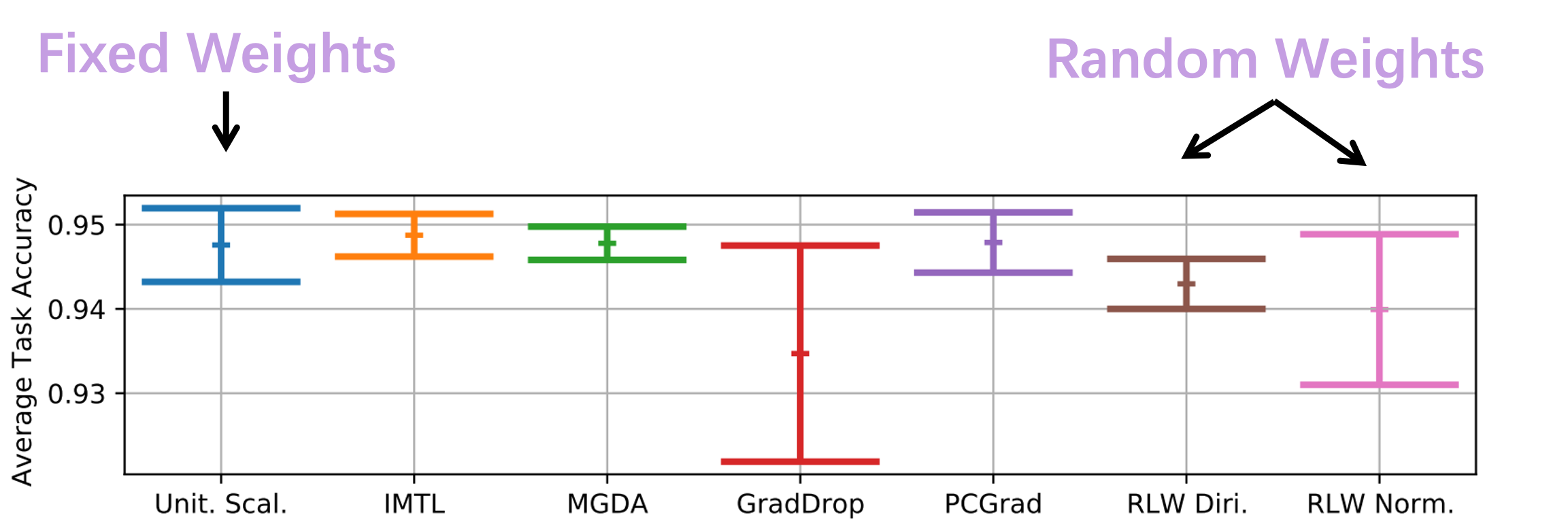
Average Accuracy on CelebA (40 Tasks)$^1$
    • The Gap: Training Loss -> Training Performance -> Testing Performance
    • A sufficiently large enough model can learn all tasks simultaneously
  • $^1$In Defense of the Unitary Scalarization for Deep MTL, NeurIPS 2022.
  • $^2$Do Current Multi-Task Optimization Methods in Deep Learning Even Help? NeurIPS 2022.
  • $^3$Reasonable Effectiveness of Random Weighting: A Litmus Test for MTL, TMLR 2022.

Future Directions

  • Task Relations:
    • Efficiently Identifying Task Groupings for Multi-Task Learning, NeurIPS 2022.
    • Auto-Lambda: Disentangling Dynamic Task Relationships, TMLR 2022.
  • Knowledge Transfer:
    • Pareto Self-Supervised Training for Few-Shot Learning, CVPR 2021.
    • Pareto Domain Adaptation, NeurIPS 2021.
  • Truely Conflicted Objectives:
    • Neural Architecture Search
    • Fairness v.s. Performance
    • Limited Capacity (e.g., on Edge Device)